Changhao Li (李昌浩)

Changhao Li (李昌浩)

M.Eng. Student

Underwater Vehicle System Identification and Navigation

Date:

Abstract

Designing underwater vehicles requires substantial time and investment. To enhance design efficiency and reduce costs, it is crucial to establish accurate, reliable, and stable simulation environments, along with robust system modeling and identification methods. These techniques improve navigation and control, enabling vehicles to adapt to various underwater conditions and tasks. Motivated by these considerations, an accurate model with six degrees of freedom (DoF) for underwater vehicle simulation is proposed in this work. We introduce an Extended Kalman Filter (EKF) to validate hydrodynamic parameters derived from computational fluid dynamics (CFD). Additionally, a Long Short-Term Memory (LSTM) neural network, recognized for its excellent performance in time-series estimation, is used to predict all linear and angular velocities. However, when applying LSTM results to dead reckoning (DR), navigation can easily diverge due to prolonged bias in attitude estimation. Hence, a non-linear complementary filter is introduced to estimate attitude accurately. Finally, validation and evaluation are conducted to demonstrate model accuracy, EKF convergence, and the reliability of LSTM-based navigation.

Modeling

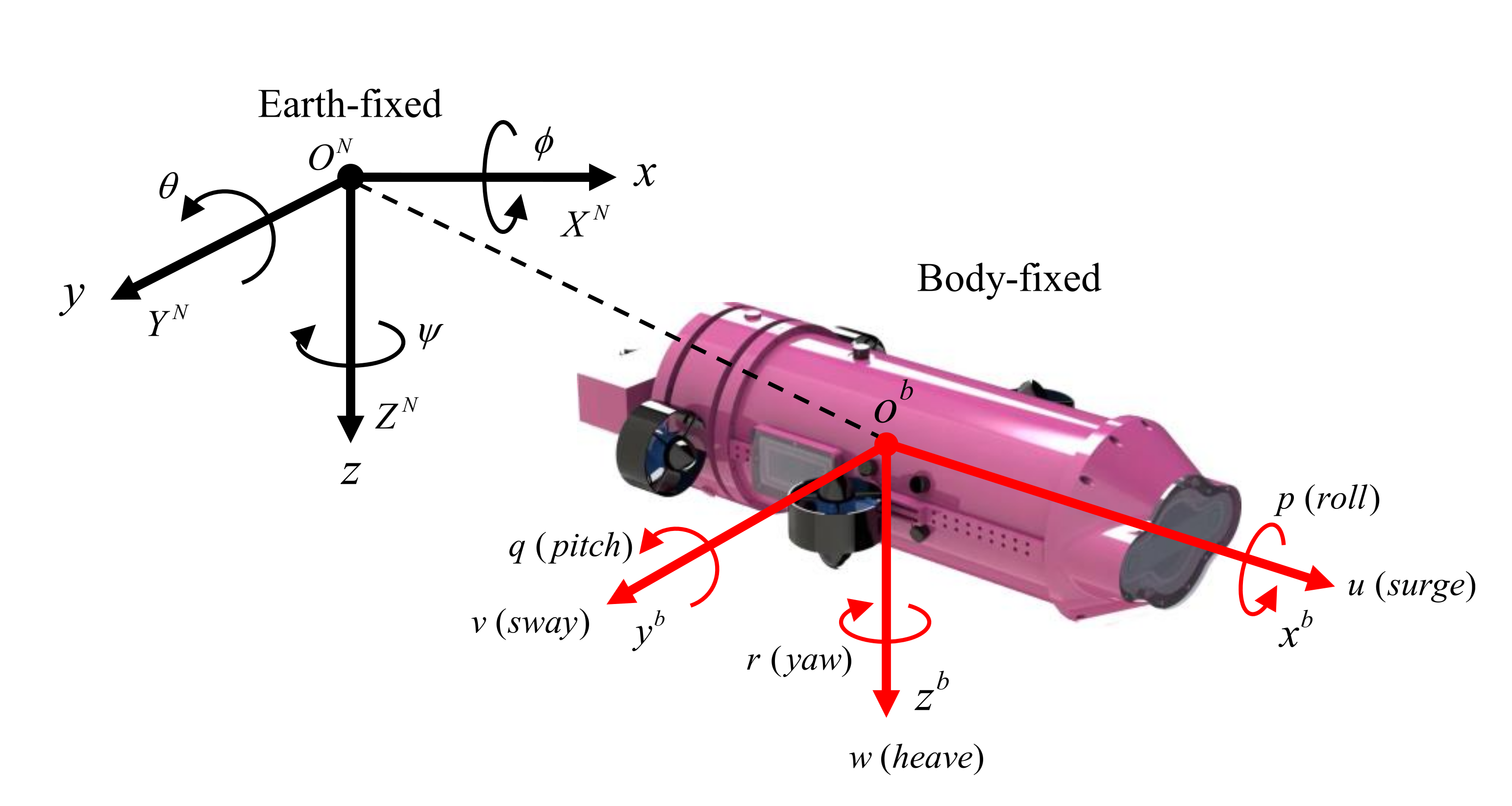
The proposed dynamic model of the underwater vehicle in this work is simplified based on the following assumptions:

  • The vehicle is symmetrical port/starboard.
  • Damping terms higher than second order are neglected.
  • Buoyancy \(B = \rho Vg\) and gravity \(W =mg\) of the vehicle are equal.
  • The center of buoyancy \(O_B = [x_B, y_B, z_B]^T\) and gravity \(O_G = [x_G, y_G, z_G]^T\) are vertically aligned on the body-fixed z-axis, i.e., \(x_G = x_B = 0\), \(y_G = y_B =0\) and \(z_G > z_B\).
  • The vehicle moves at a low speed.

When dealing with added mass \(M_A\), the assumption of \(M_A = M_A^T > 0\) as proposed by (Fossen, 1999) is not adopted. Additionally, we introduce cross-flow drag resulting from the coupling motion of sway and yaw, denoted as \(Y_{rv}\), \(Y_{vr}\), \(N_{rv}\) and \(N_{vr}\), following SNAME notation. \(\tau = Bu\), where \(B\) denotes the thrust distribution matrix, and \(u = [T_p,\ Y_s,\ T_{pv},\ T_{sv}]^T\) represents the input forces vector of all the thrusters.

coordinate
Body-fixed and earth-fixed reference frames.
\[\displaylines{ \begin{bmatrix} \dot{\nu}\\\ \dot{\eta} \end{bmatrix} = \begin{bmatrix} -M^{-1}(C(\nu) + D(\nu)) & 0_{6\times6}\\\ J_1(\eta_2) & J_2(\eta_2) \end{bmatrix} \begin{bmatrix} \nu\\\ \eta \end{bmatrix} + \begin{bmatrix} M^{-1}\\\ 0_{6\times6} \end{bmatrix} \begin{bmatrix} \tau - g(\eta) \end{bmatrix} }\]

This work focuses on analyzing and comparing the proposed port/starboard model with the second-order FS hydrodynamic model. The FS model, based on three-plane symmetry, is a commonly used model that requires only 18 hydrodynamic parameters, including 6 acceleration terms and 12 damping terms, all of which are distributed along the diagonal of the parameter matrix.

model_comparison
6-DOF nonlinear coupled model simulation result.

System Identification

Provided a detailed description of the architecture for EKF and LSTM identification, including the establishment of the dataset required for underwater vehicle model identification using LSTM, along with various operational experiments to enhance model accuracy and reliability.

Kalman Filter Hydrodynamic Parameters Identification

\[\displaylines{ x_k = x_{k-1} + \omega_{k-1} = \Theta_{26\times1} + \omega_{k-1}\\ \label{y_k} y_k = \begin{bmatrix} \nu_k\\ \eta_k \end{bmatrix} = \begin{bmatrix} \nu_{k-1}\\ \eta_{k-1} \end{bmatrix} + \begin{bmatrix} \dot{\nu}_k\\ \dot{\eta}_k \end{bmatrix} dt + v_{k-1} }\] \[\begin{split} \Theta_{26\times1} = \left[ \begin{array}{ccccccccccccc} X_u& X_{u|u|}& Y_v& Y_{v|r|}& Y_{v|v|}& Y_p& Y_r& Y_{r|v|}& Y_{r|r|}& Z_w& Z_{w|w|}& Z_q& K_v \end{array} \right.\\ \left. \begin{array}{ccccccccccccc} K_p& K_{p|p|}& K_r& M_w& M_q& M_{q|q|}& N_v& N_{v|r|}& N_{v|v|}& N_p& N_r& N_{r|v|}& N_{r|r|} \end{array} \right]^T \end{split}\]

Achieving precise accuracy for all damping terms can be challenging. To facilitate EKF convergence, we implemented phases involving one or two movements lasting around 20 seconds each. In most estimations, the EKF maintains a relatively small absolute error and exhibits high reliability in identifying hydrodynamic parameters compared to CFD results.

EKF_result
EKF estimated hydrodynamic coefficients. Disregard parameters near zero; certain coefficients associated with sway velocity fail to converge initially due to model properties.

Long Short-Term Memory System Identification

Unlike traditional neural networks, LSTM is specifically designed to handle sequential data using a cell structure chain-like loop, enabling LSTM to memorize temporal features with reduced complexity. This makes LSTM-based methods widely used in time-series analysis.

\[\displaylines{ \nu_{k} = F(\nu_{k-1},\ \eta_2,\ \tau_{k-1},\ \Delta t) }\]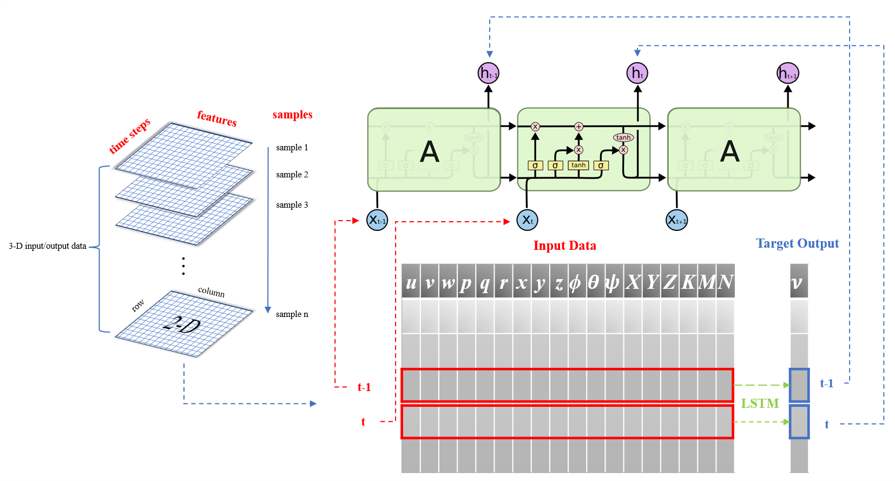
LSTM_schematics
Schematic diagram of LSTM data processing. Each plane stacked on the left represents a sampled maneuver trial reshaped into thedesired format.
LSTM_structure
Architectures of LSTM networks.

During training, we use a batch size of 1 for independent gradient calculation and parameter updates, theoretically supporting online identification. We employ the Adam optimizer to speed up convergence, training for 500 epochs with a learning rate of 0.001 and decay of 0.0001 to minimize the mean squared error (MSE) loss function. The model’s performance is validated after each epoch using the validation set. Training is conducted on a Linux PC with a 4-core Intel Core i7-4790K CPU and an NVIDIA GTX 1080Ti GPU using TensorFlow and the Keras library. The model’s accuracy and robustness are further demonstrated through the normalized error distribution of 40,000 predicted data points.

LSTM_6DoF
LSTM prediction results of 6-DoF velocity.

LSTM-based Dead Reckoning

A good way to evaluate the performance of the LSTM model is by using it to predict position through the Dead Reckoning (DR) method. The predicted position closely matches the true path. The box plot illustrates error distributions for each specific direction, with low median errors across all three axes, signifying precise dead reckoning.

\[\eta_{k} = \eta_{k-1} + J(\eta_2)\nu_{k-1} \times dt\]
LSTM_trajectory
AUV 3-D trajectory.
LSTM_boxplot
Position error box diagram.

Conclusion

Until now, we demonstrate a model-based EKF method for identifying all hydrodynamic damping coefficients without the need for specialized equipment. Additionally, we introduce a non-parametric LSTM network for navigating underwater vehicles without DVL. This work highlights the potential for parameter identification without the need for towing tank, planar motion mechanism, and rotating arm experiments, and navigation without localization sensors, particularly beneficial for small underwater vehicles with extended mission durations and demanding maneuvering needs.

This project is a work in progress, but there’s more to come!

To be continued…